Machine Learning Notes 04

Classification

  For the binary classification, $y\in {0,1 }$(Also maybe, $y\in { 0,1,2,3,\cdots}$, that’s called a multiclass classification problem, we will discuss it later.).
  So, we use a model called Logisitic Regression, and we can see the hypothesis $h_{\theta}(x)$ should value in the range of 0 and 1. This is to say, $0\leq h_{\theta}(x)\leq 1$.

Hypothesis Representation

• Logistic Regression:     $h_{\theta}(x)=g(\theta^{T}x)$, $g(z)=\frac{1}{1+e^{-z}}$

• Interpretation of Hypothesis Output. The value of $h_{\theta}(x)$ equals to the estimated probability that y=1 (on input x, parameterized by $\theta$ ). This is to say, $h_{\theta}(x)=P(y=2\mid x ; \theta)$

• Decision Boundary
  The decision boundaries are like this:

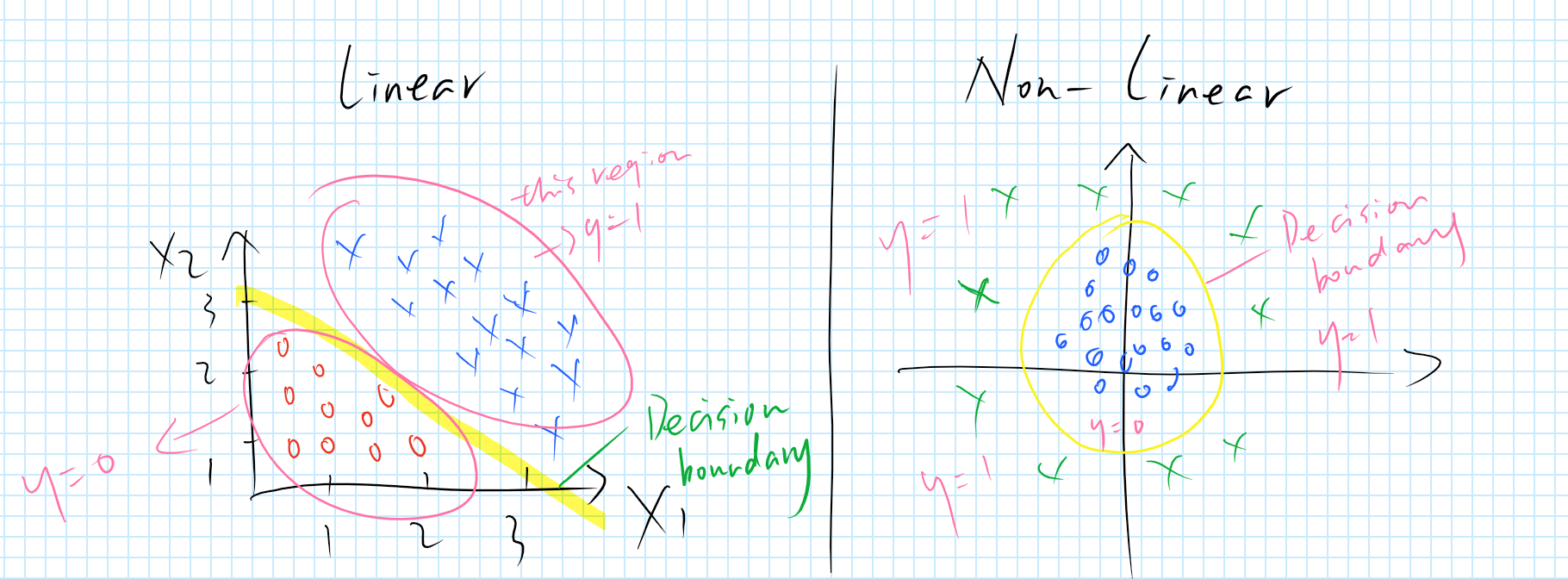
  Emphasis: Decision boundary is the property of hypothesis function, but not the property of training set and its parameters.

Logistic Regression—How to fit the parameters of theta

• Cost Function of Logistic Regression:
  $Cost(h_{\theta}, y)=-ylog(h_{\theta}(x))-(1-y)log(1-h_{\theta}(x))$

• Gradient Descent:
  To minimize $J_{\theta}$

   Repeat{
      $\theta_{j}:=\theta_{j}-\alpha\frac{1}{m}\sum_{i=1}^{n}(h_{\theta}(x^{(i)})-y^{(i)})x^{(i)}$
   }

  And we can see that this algortithm looks identical to linear regression!
  But actually, the hypothesis of them are different.
 Linear Regression: $h_{\theta}(x)=\theta^{T}x$
 Logistic Regression: $h_{\theta}(x)=\frac{1}{1+e^{-\theta^{T}x}}$

Besides,

“…use a vector rise implementation, so that a vector rise implementation can update all of these until parameters all in one fell swoop.”

Advanced Optimization

• Gradient Descent
• Conjngate Gradient
• BFGS
• L-BFGS
• ……

• Adcantages: No need to manually pick $\alpha$ ; Often faster than gradient descent;

• Disadvantages: More complex;

Multi-class classification: One-vs-all

• For example, to slove the three-class problem, we can “turn this into three seperate two-class classification problems.”
• On a new input $x$, to make a prediction, pick the class i that maximizes.